Penrose:
from mathematical notation to beautiful diagrams

Fig. 1. Penrose is a framework for specifying how mathematical statements should be interpreted as visual diagrams. A clean separation between abstract mathematical objects and their visual representation provides new capabilities beyond existing code- or GUI-based tools. Here, for instance, the same set of statements is given three different visual interpretations, via Euclidean, spherical, and hyperbolic geometry. (Further samples are shown in Fig. 29.)

Fig. 4. By specifying diagrams in terms of abstract relationships rather than explicit graphical directives, they are easily adapted to a wide variety of use cases. Here we use identical Penrose code to generate ray tracing diagrams for several targets (Sec 5.6). Though the arrangement and number of objects changes in each example, the meaning remains the same.

Fig. 7. Extensibility enables users to adopt conventions and notation that reflect the way they naturally write mathematical prose. Here, the resulting diagram plays the role of the concluding statement.

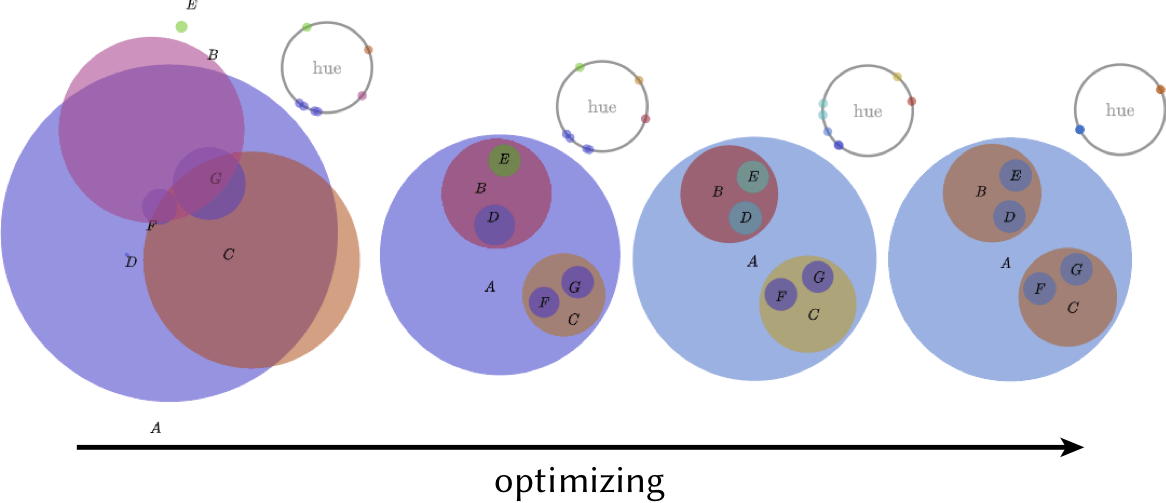
Fig. 8. An optimization-based approach makes it possible to jointly optimize visual attributes that are difficult to coordinate by hand. Here for instance we optimize color contrast according to the spatial proximity of adjacent disks (left to right), ultimately discovering a two-color solution (far right). The system can also be used to debug the optimization process itself—in this case by drawing the hue of each disk as a dot on a color wheel.

Fig. 9. A language-based design makes it easy to build tools on top of Penrose that provide additional power. Here we use standard techniques from program synthesis (Sec. 5.7) to automatically enumerate how the given relationships can be realized. Generating such examples helps to see important corner cases that might be missed when drawing diagrams by hand (where perhaps the top-left diagram most easily comes to mind).

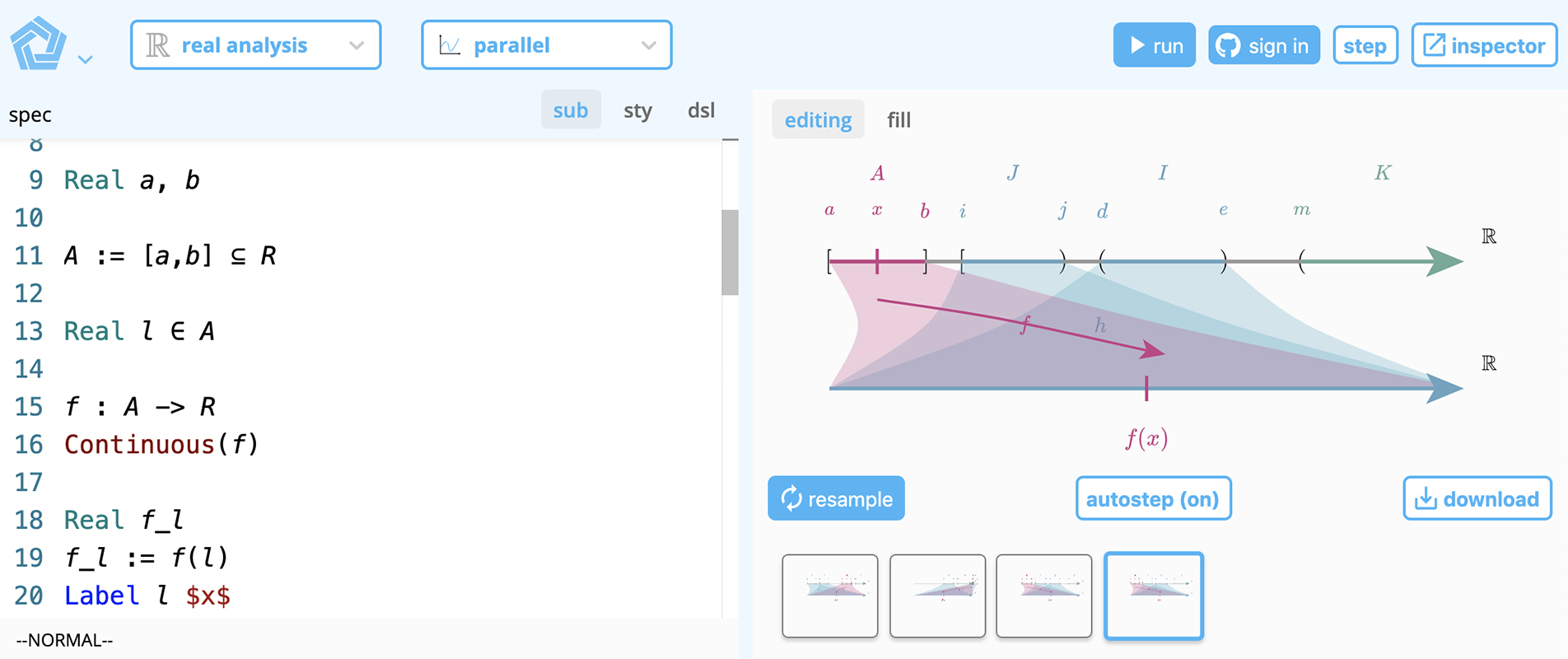
Fig. 17. Our system supports integration with web-based applications. Here a Penrose IDE provides automatic syntax highlighting and autocomplete for any user-defined domain.

Fig. 18. Here, some Substance code is used to specify set relationships. Different Style programs not only tweak the visual style (e.g., flat vs. shaded disks), but allow one to use a completely different visual representation (e.g., a tree showing set inclusions). Sets.sty above describes the flat disk style.

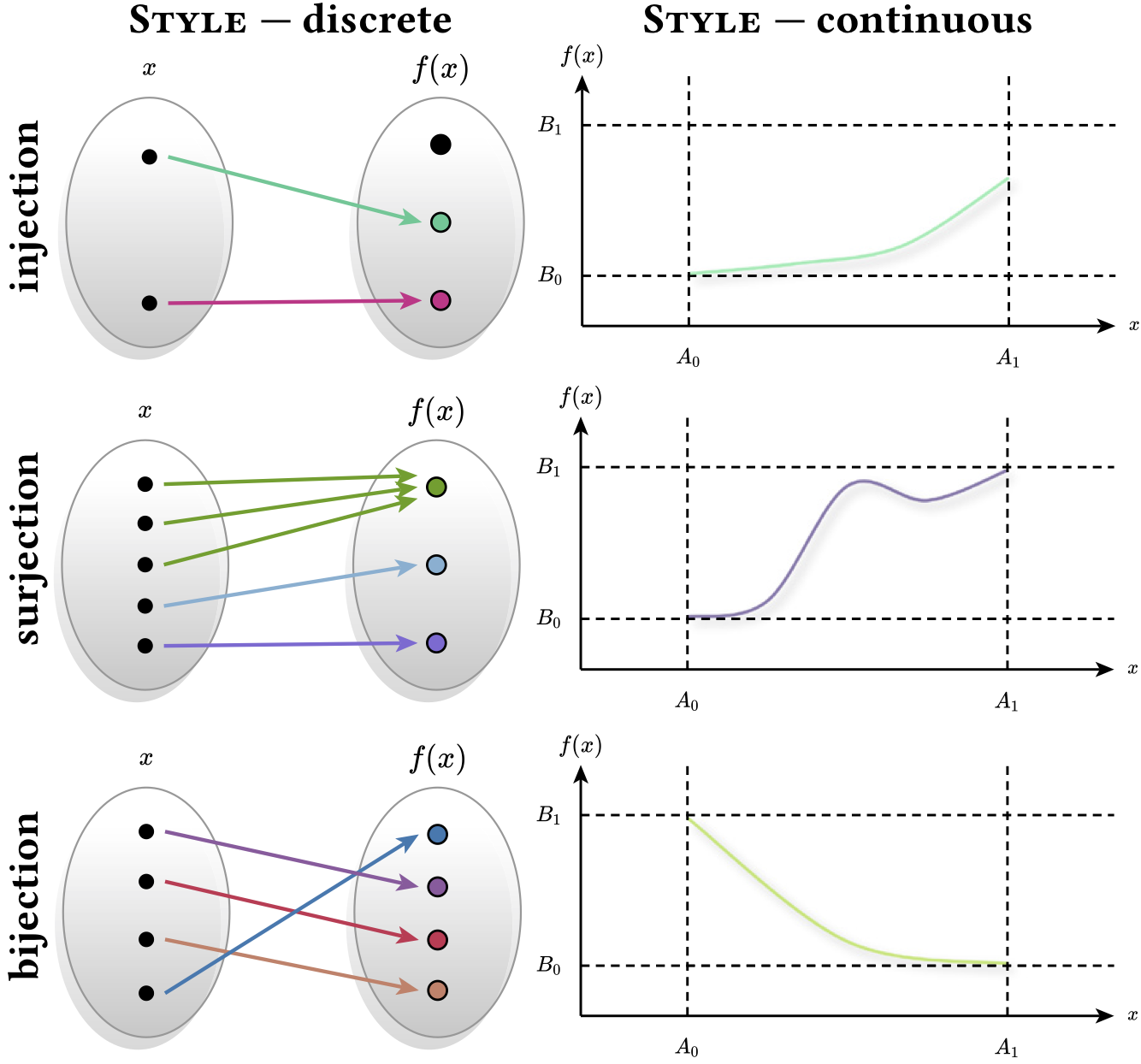
Fig. 19. Different visual representations provide different ways of thinking about an idea. Here, the notion of injections, bijections, and surjections is illustrated in both discrete (left) and continuous (right) styles. In the former, functions with the desired properties are randomly generated by an SMT solver, allowing the user to learn from many different examples.

Fig. 22. Once a complex diagram has been built, it can be easily broken into pieces or stages by, e.g., commenting out lines of Substance code. Here we illustrate steps in Euclid's proof of the Pythagorean theorem, turning Byrne's static figure (far right) into a progressive "comic strip."

Fig. 24. A language-based specification makes it easy to visually inspect data structures or assemble progressive diagrams with only minor changes to program code. Here we draw the simplicial link by building it up from simpler constituent operations.

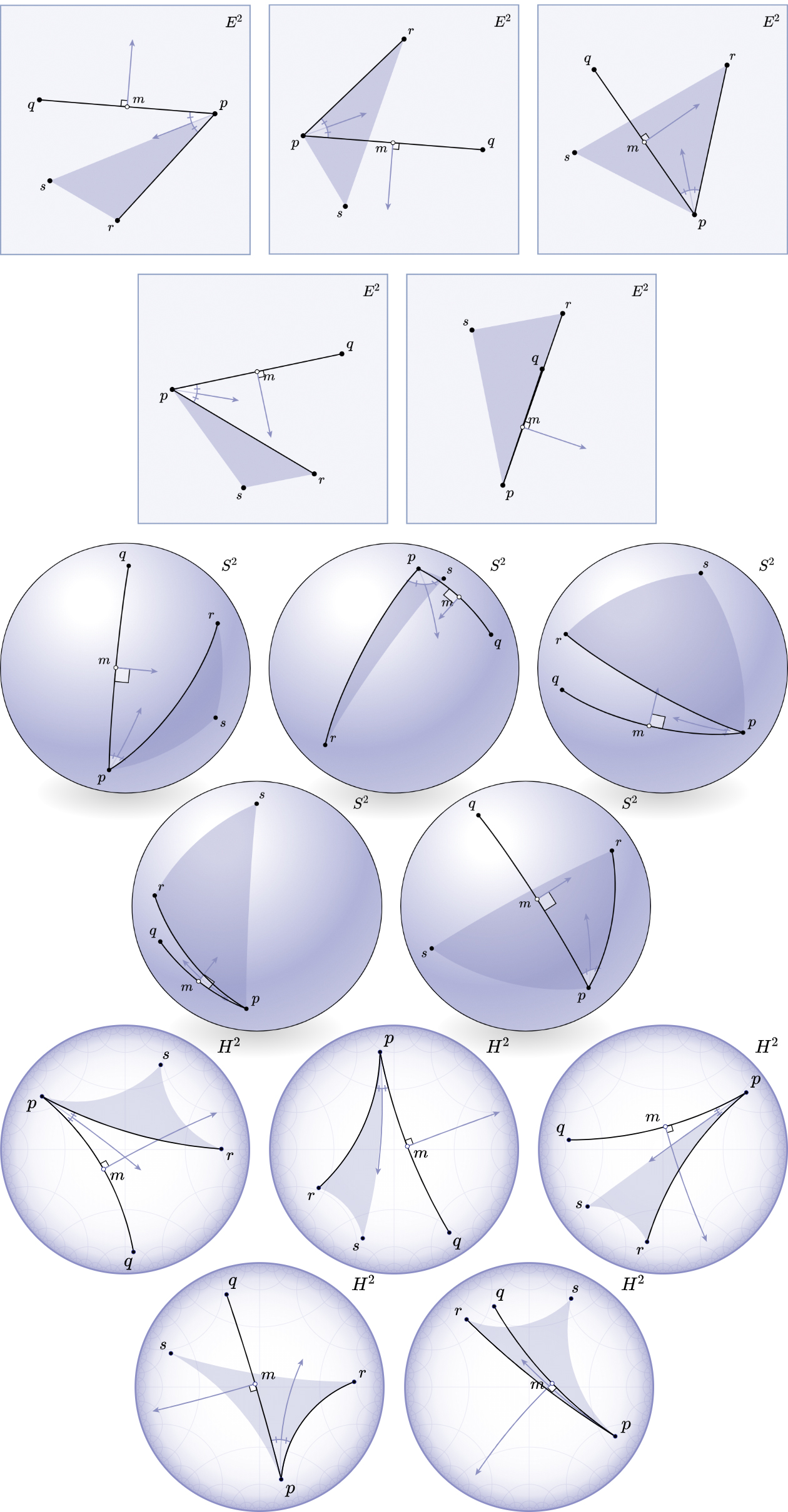
Fig. 29. Though the energy in the objective function can help guide a sampling strategy, choosing which diagram looks "best" to a given user is necessarily a subjective decision. The ability to automatically generate many alternatives makes it easier to find a satisfactory diagram. Here we show a gallery of automatically-generated variants of Fig. 1.